Combined Langmuir and ball-pen probe

This page was last updated on 7 March 2019.

#Introduction

This probe head carries a Langmuir probe and a ball-pen probe, which is an advanced probe design fathered by Jiří Adámek of the Czech Academy of Sciences. The combination of both the probes’ floating potential provides measurements of the electron temperature \(T_e\) with a higher temporal resolution that the traditional technique of sweeping a Langmuir probe can provide.

#Probe theory

The following is adapted from [Merlino, 2007].

According to the sheath theory, the current flowing through a probe is given by the sum of the electron and ion current, with both of them depending on the probe biasing voltage \(V\).

The above picture shows that in the ideal case, formulas for the ion and electron current change at the plasma potential \(\Phi\), switching from an exponential rise to saturation (no more particles can be collected from the probe vicinity per second). Thus the electron current to the probe is

\[I_e(V) = \left\{ \begin{array}{r@{\quad}c} I_{e,sat} \exp \left( \frac{V-\Phi}{T_e}\right), & V \leq \Phi \\ I_{e,sat}, & V > \Phi \\ \end{array} \right.\]

where the electron temperature is given in electronvolts. The ion current is, on the other hand,

\[I_i(V) = \left\{ \begin{array}{r@{\quad}c} I_{i,sat} \exp \left( \frac{V-\Phi}{T_i}\right), & V \geq \Phi \\ I_{i,sat}, & V < \Phi \\ \end{array} \right.\]

Now the floating potential is, due to electrons being more mobile than ions, always negative relative to the plasma potential. We also know that at the floating potential, the electron and ion current flowing to the probe are equal, yielding zero net current. Using the branches where \(V<\Phi\), this is written as

\[I_{i,sat} = I_{e,sat} \exp \left( \frac{V-V_{fl}}{T_e}\right).\]

Rearranging this equation finally yields the fundamental equation of ball-pen probe measurements:

\[\Phi = V_{fl} + \ln \frac{I_{e,sat}}{I_{i,sat}} \cdot T_e\]

The term \(\ln \frac{I_{e,sat}}{I_{i,sat}}\) is called \(\alpha\) and its value depends on the probe design, being roughly 2.8 for cylindrical Langmuir probes. The goal of the ball-pen probe is to reduce the electron saturated current which the probe can collect, and consequently reduce the \(T_e\) contribution in its floating potential. By sweeping the ball-pen probe, it has been found that \(\alpha_{BPP} = 0.6 \pm 0.3\). Thus, when the ball-pen probe floating potential \(V_{BPP}\) and the Langmuir probe floating potential \(V_{fl}\) are measured by this probe head at once, electron temperature may be inferred as

\[T_e = \frac{V_{BPP} - V_{fl}}{\alpha_{LP} - \alpha_{BPP}} = \frac{V_{BPP} - V_{fl}}{2.2}\]

#Experiments

Here are collected all experiments, reports and outputs that I was able to find on the GOLEM wiki.

• a presentantion of unknown author, background and purpose
• a collection of reports by Vojtěch Svoboda and Jan Stöckel of varying purposes
• a collection of reports by Vojtěch Svoboda and Jan Stöckel, mostly sweeping the ball-pen probe to measure its \(I-V\) characteristic, probe head installed at the bottom port
• a collection of reports by Vojtěch Svoboda, Jan Stöckel and Jiří Adámek, some sweeping of the ball-pen probe, some profiles; probe head installed at the equatorial port
• a lovely collection of reports by Vojtěch Svoboda, Jan Stöckel and Jiří Adámek, this time in readable form

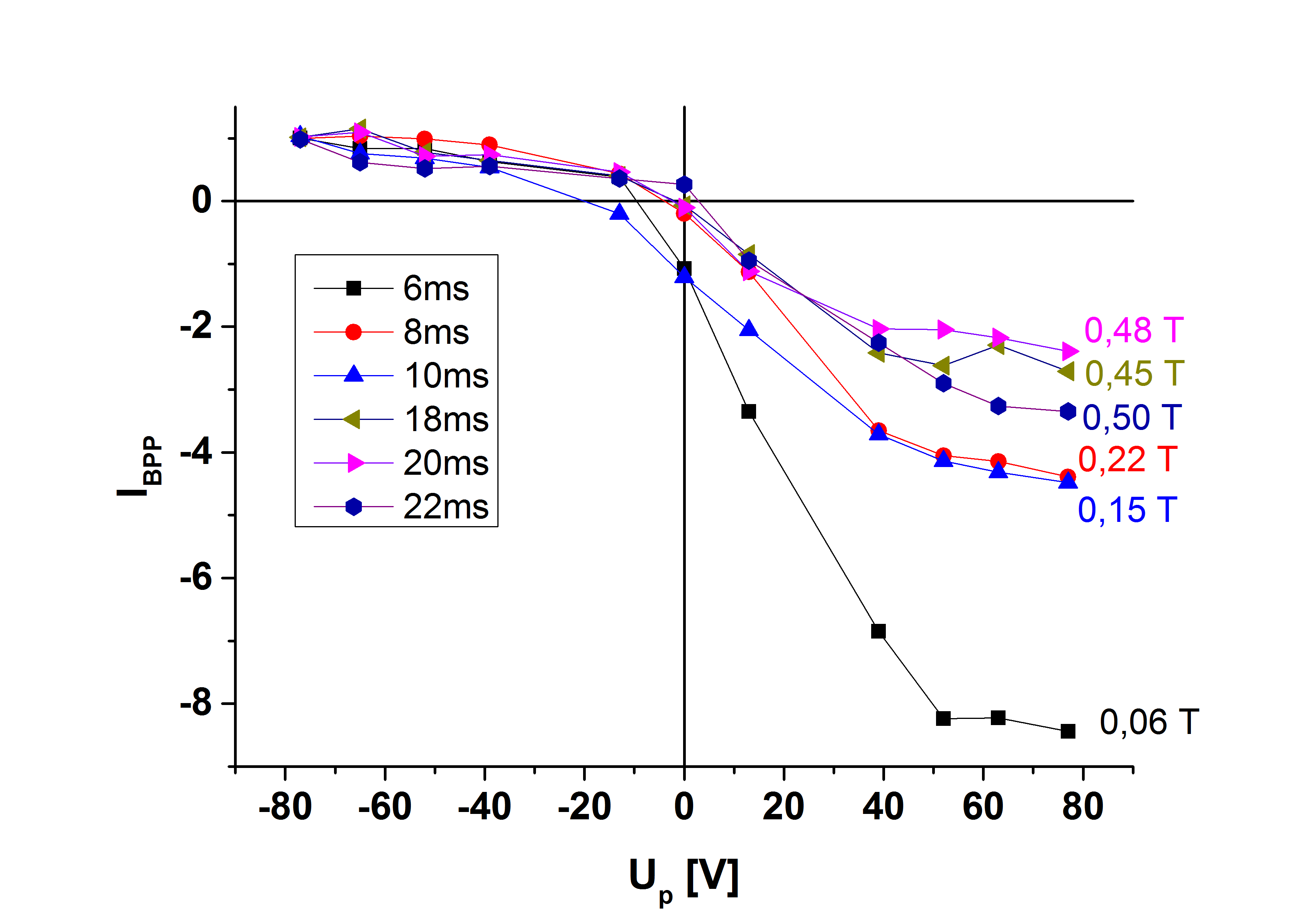
Example of the dependence of BPP \(I-V\) characteristic on magnetic field, from the collection above

• manipulator setup notes, from Spring 2017
• a short presentation on electron EEDF…?
• another short presentation, no idea what it says
• a report by Jan Stöckel, speculating why the ball-pen probe floating potential is lower than the Langmuir probe floating potential inside the port

#Literature - abstract submitted to the 44th IOP Plasma Conference: Ball-pen probe in strongly magnetised low-temperature plasmas - J. Adámek et al, A novel approach to direct measurement of the plasma potential, Czechoslovak Journal of Physics 54 (2004) - J. Adámek et al, Comparative measurements of the plasma potential with the ball-pen and emissive probes on the CASTOR tokamak, Czechoslovak Journal of Physics 55 (2005)